Las medidas con las que la inmensa mayoría de los países trata de las curvas de infectados diarios, es decir, bajar y retrasar su pico lo máximo posible para que no colapsen los sistemas sanitarios (algo que en una entrada anterior calculé que solo es posible en España si se controla infección por un espacio de cinco años), son tomadas tras analizar modelos matemáticos que recogen las características de los brotes epidémicos para realizar predicciones. Uno de los más utilizados es el (ahora) famoso modelo SIR, cuyas siglas hacen referencia a las tres curvas o grupos de población implicados en una epidemia: los susceptibles (S) de contraer la enfermedad, los infectados (I) y los recuperados (R). SIR es un modelo flexible, pero... es deductivo. Produce gráficas como la que se muestra abajo.
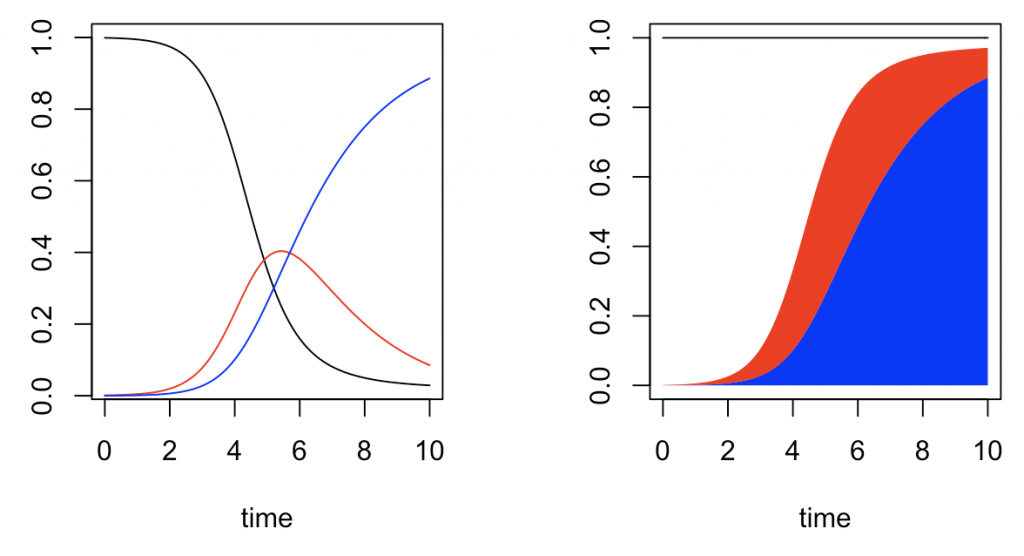
En algunas versiones los fallecidos se incluyen en R para facilitar los cálculos, si bien la mayor parte de las simulaciones las sacan del sistema.
SIR es un modelo compartimental formulado en 1911 para modelizar el avance de la malaria: se divide la población en compartimentos y se estudia cómo esta pasa de un compartimento a otro, por ejemplo de S a I y luego a R. Una de las extensiones de SIR es el modelo SEIR, que incorpora a la población expuesta (E): personas que incuban el virus de manera asintomática. Ha sido con este modelo modificado como algunos autores han evaluado que el pico de la epidemia se producirá durante la primera semana de abril, cosa a todas luces lógica si tenemos en cuanta la historicidad china y coreana del virus. Otra cuestión es cuál ese máximo.
Esta dinámica de la propagación de la enfermedad, formulada en términos de modelos ODE con la población de estudio compartimentada, tiene la siguiente formulación matemática:
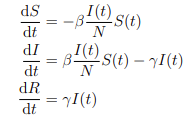
donde ya hemos dicho que S(t) representa el número de susceptibles, I(t) el número de infectados y R(t) el número de recuperados en un momento t. El tamaño de la población total es N = S (t) + I (t) + R (t), β denota la tasa de transmisión y γ denota la tasa de recuperación. En un escenario de brote, las condiciones iniciales típicas son I (0) = 1, S (0) = N - 1 y R (0) = 0.
Por lo general, queremos obtener estimaciones de β y γ. El célebre parámetro R0, número de reproducción básico (promedio de infecciones que causa un individuo contagiado), se calcula como β/γ. También hay que estimar el número inicial de individuos susceptibles. Los datos generalmente consisten en la cantidad de nuevas infecciones dentro de un cierto intervalo de tiempo, como días o semanas. La inferencia se complica entonces por el hecho de que los estados del modelo S, I, R son variables latentes y por la propia naturaleza no lineal de la dinámica de la enfermedad.
Nota: Si R0 está por debajo de 1, la epidemia irá desapareciendo. El R0 del coronavirus se encuentra entre 1,5 y 2,5, que no es demasiado alto si lo comparamos con otros virus, como el del sarampión, que tiene un valor 14 y 15. La gripe española de 1918 fue de 2,1. Alto o bajo, R0 no refleja la peligrosidad del virus, de ahí que el objetivo siempre sea conseguir que R0 sea menor que 1.
¿Se puede hacer una simulación mejor? Examinemos un brote de gripe H1N1 en un internado británico en 1978. Los datos consisten en recuentos diarios Yt del número de estudiantes infectados durante un intervalo de tiempo de 14 días. Para vincular los datos a la dinámica SIR, se puede especificar el siguiente modelo de observación de Poisson:
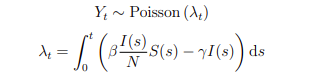
El objetivo es estimar β, γ, la proporción inicial de individuos susceptibles S(0), e implícitamente la proporción inicial de individuos infectados I(0). A priori, β puede considerarse una distribución Lognormal, γ una función Gamma y S(0) una distribución Beta.
Esta anterior aproximación es determinista y suele dar buenos resultados porque da una idea de la dinámica de la enfermedad. Sin embargo, considerar la estocasticidad demográfica permite una estimación más precisa de los parámetros relacionados con la propagación de la enfermedad, pues esta componente estocástica (es decir, los parámetros evolucionan al azar con el tiempo) absorbe los errores introducidos en el modelo determinista. O incluso podemos suponer que cada cepa del virus actúa de forma independiente. Es lo que se conoce como modelo multistrain:
donde Sx (t) indica el número de susceptibles a la cepa x en el tiempo t y de manera similar Ix (t) y Rx (t) denotan el número de individuos infectados y recuperados a la cepa x en el tiempo t. El modelo consta de compartimentos superpuestos, con un tamaño de población total (N = Sx(t) + Ix(t) + Rx(t)) para cualquier cepa x. βx es la velocidad de transmisión específica de la cepa y γ es la velocidad de recuperación, modelada como idéntica para cada cepa.
Este modelo multistrain se adoptó para modelar la expansión del virus de la gonorrea en el Reino Unido:
El número total de casos de gonorrea reportados entre 2012 y 2016 se muestra en la imagen de arriba por edad (eje x), sexo (filas) y tres regiones (columnas) de Inglaterra: Este de Inglaterra, Londres y el Sudeste de Inglaterra. Hubo sustancialmente más casos reportados entre los hombres. Los ajustes del modelo multistrain fueron los siguientes:



No hay comentarios:
Publicar un comentario